In questo post parleremo del teorema più famoso della geometria: il teorema di Pitagora. Come prima cosa vedremo l’enunciato e tutte le formule utili per applicare il teorema di Pitagora a problemi concreti di geometria piana (e non solo). Successivamente ne daremo una interpretazione grafica, che sono sicuro non dimenticherete mai. Il tutto condito da un po’ di curiosità storiche che troverete a conclusione dell’articolo.
Enunciato del teorema di Pitagora
Il teorema di Pitagora si applica ai triangoli rettangoli, ovvero a tutti quei triancoli che presentano almeno un angolo interno retto (equivalentemente, un angolo di 90 gradi). L’enunciato del teorema di Pitagora esprime una relazione tra l’ipotenusa (il lato opposto all’angolo retto) ed i cateti (i restanti due lati). Ecco l’enunciato del teorema di Pitagora:
In ogni triangolo rettangolo, il quadrato costruito sull’ipotenusa è uguale alla somma dei quadrati costruiti sui cateti.
ENUNCIATO DEL TEOREMA DI PITAGORA
Nota bene che quando nell’eneunciato viene nominato il “quadrato” costruito su ipotenusa o cateto, si sottintende che la quantità presa in considerazione è l’area di questo quadrato.
Formule matematiche del teorema di Pitagora: diretta e inversa
Vediamo immediatamente come l’enunciato del teorema di Pitagora viene espresso in formule sintetiche e facili da ricordare. Indicando con \(i\) il valore dell’ipotenusa, con \(c\) il valore di un cateto e con \(C\) il valore del secondo cateto, l’enunciato può essere descritto dalla seguente formula (diretta) del teorema di Pitagora:
\(i^2 = c^2 + C^2\)Come vedi, provando a leggere la formula matematica in linguaggio comune, possiamo dire che “ipotenusa al quadrato è uguale al primo cateto al quadrato più il secondo cateto al quadrato”. Coincide esattamente con l’enunciato, non è vero?
Nei problemi di geometria che vengono assegnati a scuola, spesso è necessario trovare il valore dell’ipotenusa. D’altro canto nella formula sopra, viene descritto come calcolare l’ipotenusa al quadrato. Per calcolare l’ipotenusa \(i\), è sufficiente utilizzare la seguente formula per calcolare l’ipotenusa derivante dal teorema di Pitagora:
\(i = \sqrt{c^2 + C^2}\)Per calcolare il valore dei cateti, invece, dobbiamo utilizzare le formule inverse del teorema di Pitagora. Esse sono molto simili per entrambi i cateti. Infatti è completamente arbitraria l’assegnazione del “primo” cateto e del “secondo” cateto. Alcuni preferiscono riferirsi ai due cateti come al “cateto minore” (quello di lunghezza inferiore) e “cateto maggiore” (quello di lunghezza maggiore). È importante notare, però, che in un caso particolare i cateti possono avere la stessa lunghezza.
Di seguito trovate le formule per calcolare i cateti derivanti dal teorema di Pitagora:
\(c = \sqrt{i^2 – C^2}\) \(C = \sqrt{i^2 – c^2}\)Come certamente avrai notato, le due formule sono molto simili ed interscambiabili.
Interpretazione grafica del teorema di Pitagora
Per interpretare graficamente il teorema di Pitagora, adesso disegneremo un triangolo rettangolo e coloreremo i quadrati costruiti sui suoi lato in modo diverso. Bada bene, l’ipotenusa è sempre il lato più lungo, che si trova di fronte all’angolo retto.
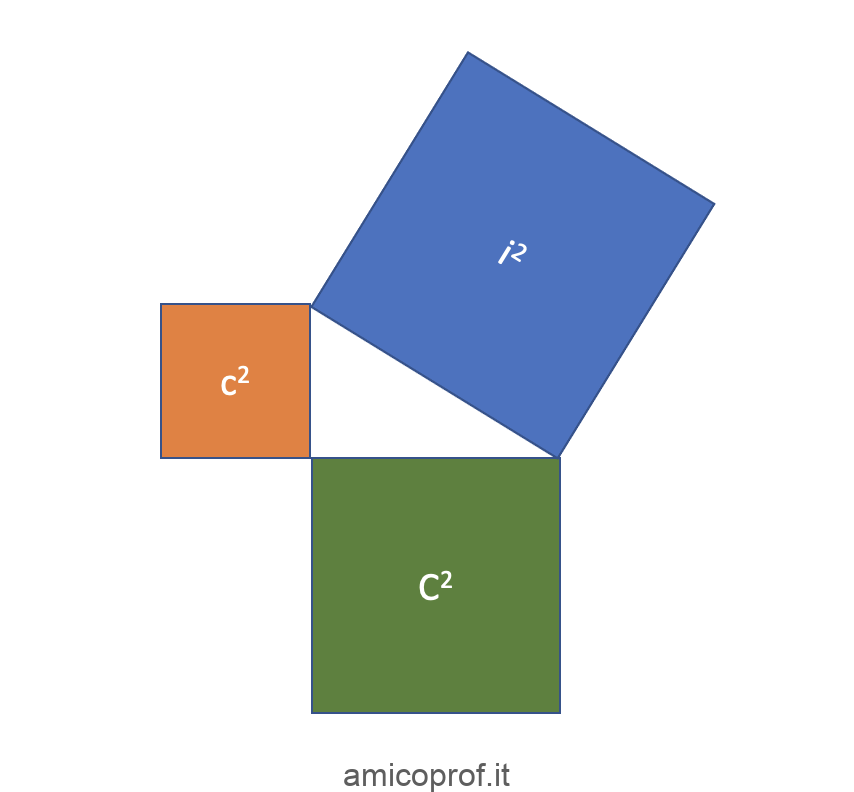
Il teorema di Pitagora che abbiamo enunciato precedentemente definisce una relazione tra questi quadrati. In particolare esso ci dice che il quadrato costruito sull’ipotenusa (il quadrato blu nella nostra figura) è uguale alla somma dei quadrati costruiti sui cateti (nella nostra figura essi sono colorati in arancione e verde). Come esprimere questa proprietà enunciata dal teorema di Pitagora graficamente? Semplicissimo: allineamo i quadrati ed inseriamoli in una equazione matematica, come illustrato nella successiva figura.

Curiosità storiche sul teorema di Pitagora
Spero che a questo punto ti sia chiaro il significato del teorema di Pitagora e cosa questo significa nella geometria piana dei triangoli rettangoli. Tieni a mente che tale teorema non è utile solo nel caso dei triangoli rettangoli. Infatti, in molti problemi che coinvolgono altre figura geometriche, spesso vengono dati come informazioni soltanto alcune proprietà della figura, come per esempio un angolo interno ad un poligono qualsiasi. Bene: se quest’angolo è retto (di 90 gradi) avrai quasi sicuramente la possibilità di applicare il teorema di Pitagora per determinare la lunghezza di una sua dimensione.
Alcune curiosità storiche. Il teorema di Pitagora viene spesso attribuito al filosofo e matematico Pitagora (495 a.C.). La sua origine è, però, certamente più antica. I babilonesi conoscevano il teorema e lo utilizzavano nella pratica quotidiana. Alcuni scritti cinesi antecedenti almeno mille anni la nascita di Pitagora, rivelano che il teorema era conosciuto anche da quelle parti. Situazione analoga in India. Non ci sono invece prove certe che questa conoscenza fosse anche disponibile agli egizi in quanto nessuna informazione riguardante il teorema di Pitagora è stata rinvenuta tra gli scritti matematici di quella civiltà.
