Ti sarà capitato spesso di sentire delle frasi del tipo:
“10 è divisibile per 2”
oppure:
“13 è divisibile solo per 1 e per se stesso”.
Ma cosa significa esattamente divisibile? In matematica, la divisibilità è una proprietà dei numeri interi. Per numeri interi si intendono tutti quei numeri senza decimali (o meglio, con parte decimale nulla). Esempi di numeri interi sono: \( …, -3, -2, -1, 0, 1, 2, 3, …, 100, … \)
Tecnicamente, si dice che un numero intero N è divisibile per un altro numero intero M se la divisione N/M dà come resto zero.
DEFINIZIONE MATEMATICA
Ma passiamo ad un esempio concreto per non perderci con le definizioni generali con i letterali N ed M.
Prendiamo i numeri 10 e 2. La divisione 10/2 = 5 con resto 0. Questo significa che possiamo affermare che 10 è divisibile per 2.
Divisibilità: un esempio geometrico
Possiamo anche vederla in un modo più pratico, usando la geometria. Quante volte riesco a far entrare un segmento di lunghezza 2 in uno spazio di 10? L’immagine qui sotto può darci una mano:
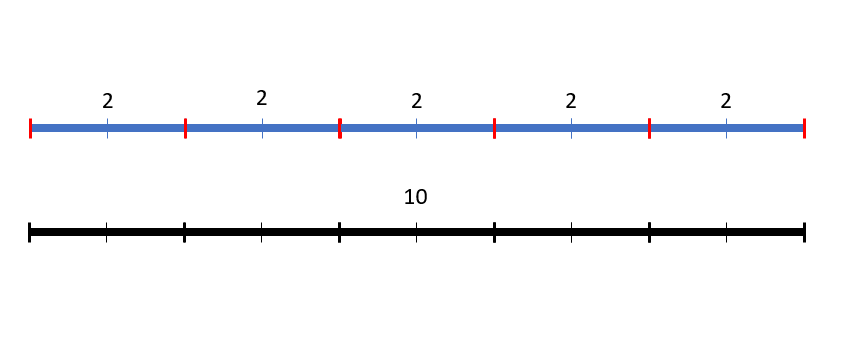
Dall’immagine possiamo vedere che in uno spazio di lunghezza 10 sono in grado di posizionare ben 5 segmenti di lunghezza 2. Nessuna parte dei segmenti di lunghezza 2 eccede lo spazio, ma rientrano perfettamente. Questo è vero in quanto 10 è divisibile (o suddivisibile) in elementi da 2.
Quando invece non vale la divisibilità, noteremo che non siamo in grado di riempire con la stessa precisione lo spazio dato. Prendiamo per esempio i numeri 9 e 2. La divisione 9/2 = 4 con resto 1. Il numero 9 non è quindi divisibile per 2, come possiamo notare anche dall’esempio qui sotto:
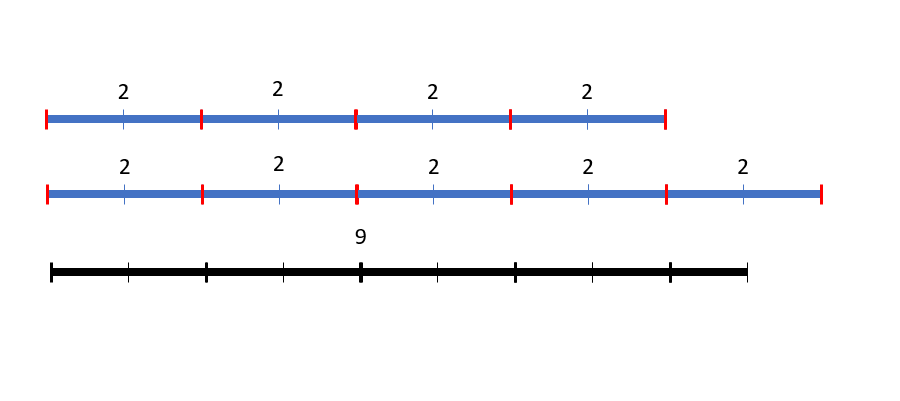
In questo nuovo esempio geometrico, quattro segmenti da 2 non sono sufficienti a ricoprire lo spazio grande 9, mentre cinque segmenti eccedono lo spazio.
Spero che questo post ti abbia aiutato a comprendere la nozione matematica di divisibilità. Se qualcosa ti è sfuggito o hai delle altre domande, scrivi qui sotto tra i commenti oppure inviaci una email.