Disequazioni: Soluzioni Interne o Soluzioni Esterne?

Nelle disequazioni di secondo grado generalmente il primo passo da compiere è quello di trovare le soluzioni dell’equazione di secondo grado associata. Ragionando in termini generali, data una disequazione del tipo:

\(a x^2 + b x + c > 0\) oppure \(a x^2 + b x + c < 0\)

come prima cosa, troveremo le soluzioni dell’equazione associata

\(a x^2 + b x + c = 0\).

Chiaramente, i coefficienti \(b\) e \(c\) potrebbero essere nulli. L’equazione avrebbe in tal caso dei “termini in meno”. Il coefficiente \(a\), invece, lo assumiamo diverso da zero: in caso contrario avremmo a che fare con una disequazione di primo grado.

Per trovare le soluzioni dell’equazione associata, procediamo come al solito calcolando il delta. Generalmente (quando il delta è positivo), per una equazione di secondo grado otteniamo due soluzioni distinte, che indichiamo con \(x_1\) ed \(x_2\). Per i casi di delta nullo e negativo, guarda questo altro post.

Per capire se la soluzione della disequazione originale è per valori interni o per valori esterni, guarderemo al segno del coefficiente \(a\) ed al segno della disequazione.

Per delta positivo (o maggiore di zero) avremo due soluzioni distinte che indicheremo con \(x_1\) ed \(x_2\):

Per i più curiosi, però alcune domande potrebbero ancora aver bisogno di una risposta. In tal caso, continuate la lettura di questo articolo.

Perché per segni concordi la disequazione ha soluzione per valori esterni (e viceversa)? Spiegazione geometrica.

Per rispondere a questa domanda, faremo uso della geometria analitica. Un polinomio di secondo grado rappresenta sul piano cartesiano una curva geometrica chiamata parabola. Per scoprire che forma ha una parabola, prova a considerare la seguente funzione:

\(y = a x^2 + b x + c \)

e disegna tanti punti sul piano cartesiano, al variare di \(x\). Alla fine di questo processo otterrai una figura simile a questa:

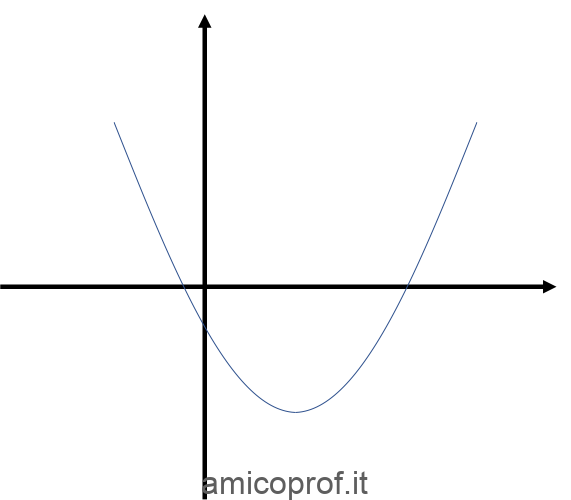
Su questa figura geometrica, ci sono due cose interessanti da sapere:

1. Le soluzioni dell’equazione associata corrispondono all’intersezione della curva parabolica con l’asse orizzontale.
2. Il segno del coefficiente del termine di secondo grado determina se la concavità è verso l’alto (\(a>0\)) o verso il basso (\(a<0\)).

Conoscendo queste nuove informazioni, è facile capire come mai per segni concordi (per esempio, \(a>0\) ed una equazione in “\(>\)” (maggiore) ) dobbiamo prendere soluzioni esterne. Infatti, l’esempio corrisponde ad una parabola con concavità verso l’alto (come quella in figura) che ha valori maggiori di zero (rispetto all’asse delle y) nei “bracci” esterni alle soluzioni (ovvero, esterni rispetto ai punti in cui la curva interseca l’asse delle \(x\) ).

Come prendere soluzioni interne od esterne quando il delta è nullo o negativo?

Rispolverando le nostre competenze sulle equazioni di secondo grado, sappiamo che in funzione del valore del delta si possono presentare tre situazioni distinte.

• Se il \(\Delta>0\) (delta positivo), otterremo due soluzioni diverse, ovvero \(x_1\ne x_2\).
• Se il \(\Delta=0\) (delta nullo, ovvero delta uguale a zero), otterremo due soluzioni coincidenti, ovvero \(x_1= x_2 \).
• Se il \(\Delta<0\) (delta negativo), l’equazione non ammette soluzioni reali.

Consideriamo allora di due casi singolarmente e costruiamo la tabella delle soluzioni in maniera simile a quanto fatto per il primo caso con delta maggiore di zero.

Per delta zero (o delta nullo) avremo una unica soluzione che indicheremo con \(x_{1,2}\):

Per delta negativo l’equazione non ammette soluzioni (reali). Avremo dunque che:

Spero che questo post vi sia stato utile a risolvere il vostro esercizio ma soprattutto ad imparare qualcosa di nuovo. È sempre divertente quando si riesce a comprendere la motivazione che sta dietro ad una regola, per questo spero che abbiate avuto la pazienza di andare oltre le tabelle riassuntive e leggere il paragrafetto con la spiegazione in termini geometrici. La tabella la dimenticherete in poco tempo, la spiegazione non la dimenticherete mai! (Io stesso l’ho imparata così).