Le equazioni differenziali ordinarie non sono altro che equazioni dove l’incognita è una funzione e i cui termini sono le derivate della funzione stessa; ovviamente, per fare ciò, la funzione deve essere derivabile un numero sufficiente di volte.
Per capire a cosa servono le equazioni differenziali prendo in considerazione un esempio, ovvero prendiamo una massa y(t) al tempo t; dopo un certo tempo trascorso, quindi sicuramente ora parleremo di una variazione di tempo; questa massa avrà subito una deformazione e può essere che inizi a consumarsi in modo proporzionale.
Quindi quello che vogliamo andare a capire, sarà quello di sapere la massa che avremo dopo tale variazione di tempo; dato che la massa avrà anch’essa subito una trasformazione. Questo lo possiamo vedere in questa foto:
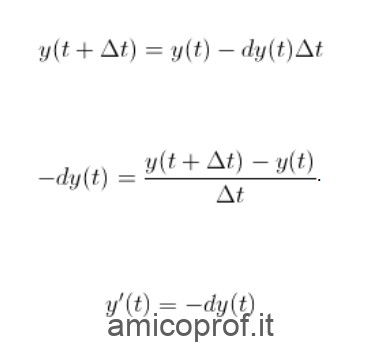
Durante gli studi andiamo ad analizzare tali equazioni differenziali a cui diamo un preciso valore ad alcune delle variabili in gioco; in particolare la funzione incognita e le sue derivate un’equazione in forma normale di ordine in certi punti del dominio di definizione dell’equazione.
Il problema differenziale che ne risulta è detto “problema di Cauchy”; consiste solitamente nel porre delle condizioni iniziali o delle condizioni di contorno per gli estremi del dominio in cui è definita l’equazione.
Ovviamente, per qualsiasi altra informazione più dettagliata vi lascio il link di Wikipedia dove sicuramente troverete molte più informazioni: https://it.wikipedia.org/wiki/Equazione_differenziale