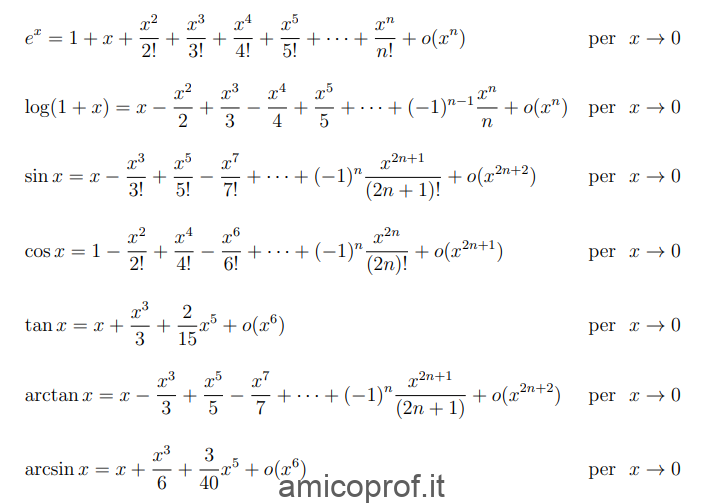Il calcolo dei limiti è un’operazione che permette di studiare il comportamento di una determinata funzione però valutata nell’intorno di un punto o all’infinito.
Detto in maniera differente questo ci consente di determinare il valore a cui tende una funzione per poi poter graficare la funzione stessa.
Esistono vari metodi per svolgere tali limiti, ad esempio nel primo esercizio così come nel secondo ci siamo ritrovati ad una forma indeterminata del tipo 0/0 dove ho applicato de l‘Hôpital, ma al tempo stesso ho usato la serie di Taylor e i limiti notevoli, tutti metodi accettabili per svolgere tali limiti.
Il teorema di de l‘Hôpital è un teorema sui limiti di funzioni reali di variabile reale che consente di calcolare il limite di un rapporto di funzioni facendo la derivata del numeratore e quella del denominatore separatamente.
Invece, la serie di Taylor di una funzione in un punto è la rappresentazione della funzione come serie di termini calcolati a partire dalle derivate della funzione stessa nel punto.
Queste sono le serie di Taylor più note: